
The Addition Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality. The Elimination Method is based on the Addition Property of Equality. Solve a System of Equations by Elimination This is what we’ll do with the elimination method, too, but we’ll have a different way to get there. When we solved a system by substitution, we started with two equations and two variables and reduced it to one equation with one variable. The third method of solving systems of linear equations is called the Elimination Method. Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression. Graphing works well when the variable coefficients are small and the solution has integer values. We have solved systems of linear equations by graphing and by substitution. If you missed this problem, review Example 2.48. Word problems on sum of the angles of a triangle is 180 degreeĭomain and range of rational functions with holesĬonverting repeating decimals in to fractionsĭecimal representation of rational numbers
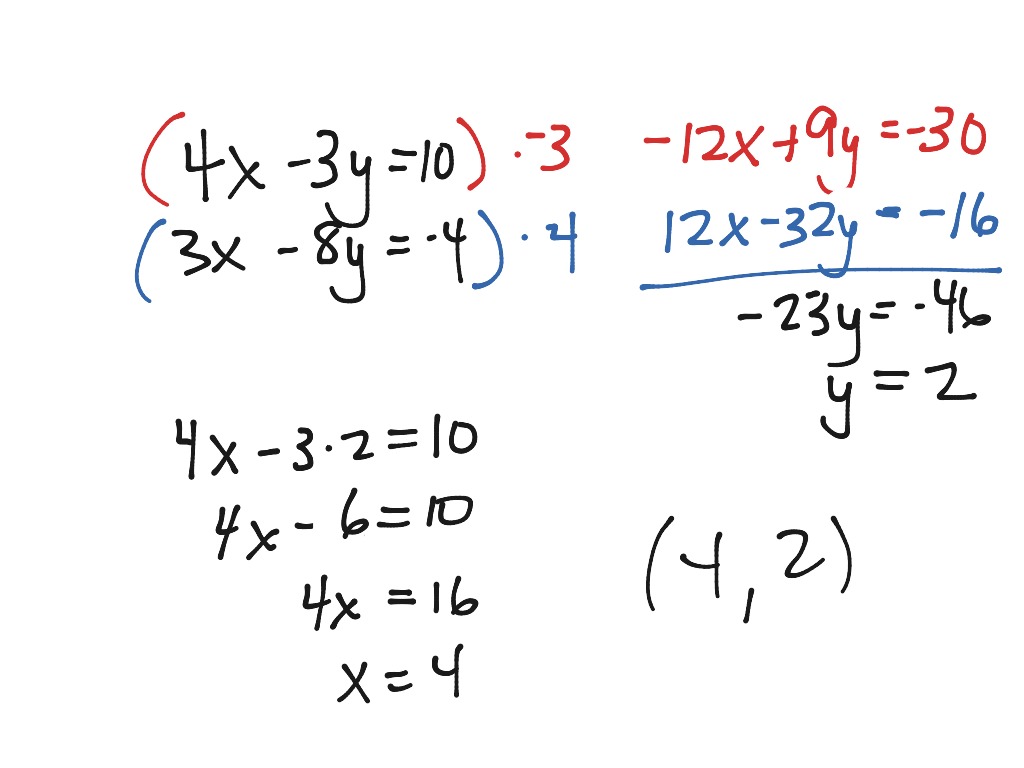
Word problems on direct variation and inverse variationĬomplementary and supplementary angles word problems Sum of the angle in a triangle is 180 degreeĭifferent forms equations of straight lines Trigonometric ratios of supplementary anglesĭomain and range of trigonometric functionsĭomain and range of inverse trigonometric functions Trigonometric ratios of complementary angles Trigonometric ratios of angles greater than or equal to 360 degree
SOLVING EQUATION SYSTEMS BY ELIMINATION PLUS
Trigonometric ratios of 270 degree plus theta Trigonometric ratios of 270 degree minus theta Trigonometric ratios of 180 degree minus theta Trigonometric ratios of 180 degree plus theta

Trigonometric ratios of 90 degree plus theta Trigonometric ratios of 90 degree minus theta Trigonometric ratios of some negative angles Trigonometric ratios of some specific angles Nature of the roots of a quadratic equation worksheetsĭetermine if the relationship is proportional worksheet Writing and evaluating expressions worksheet Quadratic equations word problems worksheetĭistributive property of multiplication worksheet - Iĭistributive property of multiplication worksheet - II Proving trigonometric identities worksheet Special line segments in triangles worksheet Sum of the angles in a triangle is 180 degree worksheet Sum and product of the roots of a quadratic equationsĬomplementary and supplementary worksheetĬomplementary and supplementary word problems worksheet Nature of the roots of a quadratic equations Solving quadratic equations by completing square Solving quadratic equations by quadratic formula Solving linear equations using cross multiplication method Solving linear equations using substitution method Solving linear equations using elimination method So we can eliminate the variable y by adding the two equations.

And also, the variable y is having different signs. In the given two equations, the variable y is having the same coefficient. Solve the system of equations using elimination method. Now add the two equations to eliminate the variable. If not, multiply one of the equations by negative sign. The variable which is eliminated must have different signs. If not, make them to be same using least common multiple and multiplication. The variable which is eliminated must have the same coefficient in both the equations. The following steps will be useful to solve system of equations using elimination method. In this method, one of the variables is eliminated by adding or subtracting the two equations of the system to obtain a single equation in one variable. The elimination method can be used to solve a system of linear equations.


 0 kommentar(er)
0 kommentar(er)
